Számlogikai rejtvények szabályai
Sudoku
Tömbök nélkül (Latin négyzet)
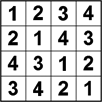 | A Latin négyzet egy n-szer n-es nagyságú táblázat amiben n számú különböző számjegy van kitöltve, minden számjegy pontosan egyszer szerepel minden sorban és minden oszlopban. Latin négyzet szabály:
|
Téglalap tömbök
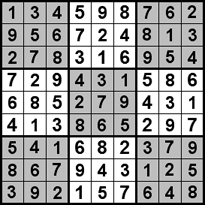 | A legelterjedtebb forma a Téglalap alakú hasáb. A 9x9-es rács 9 hasábból áll, mint ahogy a képen látható. Téglalap hasábok szabályai:
|
Szabálytalan tömbök (jigsaw)
 | A Jigsaw-kirakós rejtvényt ugyanúgy játsszák, mint a Szúdokut, azt kivéve, hogy a rácsban szabálytalan tömbök vannak, más néven ketrecek. Irregular Blocks-szabálytalan tömbök szabályok:
|
Diagonal Variants - Átlós verzió
 | Elterjedt, hogy a számjegyek elhelyezkedésének korlátait megadják, a rendes sorok és oszlopok között. Az egyik ilyen korlátozás az átlós verzió. Diagonal Variants - Átlós variáció szabály:
|
Kombinált variáció:
 | A variációkat lehet keverni. Például: a rácsban lehetnek Derékszögű tömbök és átlós vonalak is. Lehet több, mint 2 átlós vonal is. Derékszögű tömbök és Átlós variáns szabályok:
|
Átfedő variációk
Az Átfedéses variáció néhány rejtvényből áll. A megosztott tömbök eltérő színnel vannak kiemelve. Itt van néhány példa az átfedéses Szúdokukra:
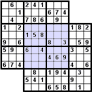
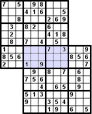
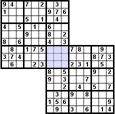
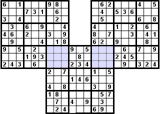
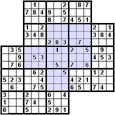
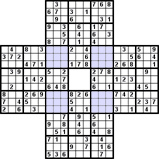
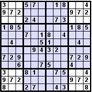
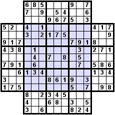
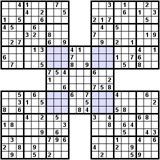
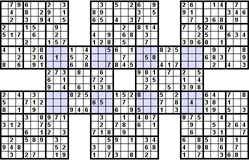
Gyilkos
 | A Gyilkos Szúdoku rácsa el van el van lepve ketrecekkel (cellák csoportjával), pontozott körvonallal van jelölve. Az egyes ketrecek 2 vagy több cellát foglalnak magukba. A bal felső cella felirata a ketrec összege, ami az összege a megoldás számjegyeinek a ketrec összes celláján belül. Gyilkos szúdoku szabályok:
|
Nagyobb/Kisebb
 | A nagyobb, mint (vagy kisebb, mint) Szúdokuban nincsenek megoldó kulcsok(számjegyek) megadva. Helyette vannak "nagyobb, mint" (>) vagy "kisebb, mint" (<) relációs jelek jelölik, hogy a számjegy egy cellában nagyobb kell, hogy legyen vagy kisebb a másiknál. Nagyobb, mint / Kisebb, mint szabályok:
|
Kakuro
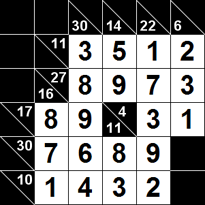 | A Kakuro (Kakkuro) rejtvény rácsában vannak előre kitöltött mezők, feketék és fehérek rendszerint. A rács fel van osztva bejáratokra (a fehér mezők vonalai) a fekete mezők által. A fekete mezők tartalmaznak egy ferde vonalat a bal-fentről jobbra-le és számot egy vagy mindkét félben. Ezeket a számokat "megoldó kulcsoknak" hívják. Kakuro szabály:
|
Kalkuldoku
 | A rács felosztott vastag határvonalak ketrece (mezők csoportja) által. A számok a mezőkben az egyes ketrecekben kell hogy eredményezzék a bizonyos "célszámot" amit meghatározott számtani művelet (akár összeadás, kivonás, szorzás vagy osztás) használatával érünk el. Kalkuldoku szabályok:
|
Futoshiki
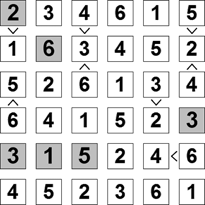 | A Futoshiki olyan játék, hogy a rácsban már meg lehet adva a játék kezdetén néhány számjegy. Továbbá relációs jelek "nagyobb, mint" (>) vagy "kisebb, mint" (<) a szomszédos cellák között. amely jelöli, hogy a számjegy az adott cellában nagyobbnak vagy kisebbnek kell lenni a másiknál. Futoshiki szabályok:
|
Straights
 | A Straights-et olyan rácsban játsszák ami részlegesen el van választva fekete cellákkal részekre. A részeknek egyenes vonalat kell tartalmazniuk - egymást követő számok sorát - de bármilyen rend szerint (például: 2-1-3-4). Lehetnek fehér négyzetek is a fekete cellákban. Straights szabályok:
|
Felhőkarcoló
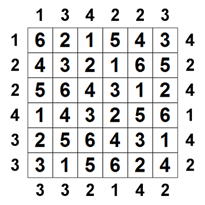 | A Skyscraper rejtvénynél számok vannak a rács mentén. Azok a számok mutatják meg, az épületek számát amit te láthatsz abból az irányból a fehőkarcolók sorozatában, a legmagasabb elemek magassága megegyezik abban a sorban vagy oszlopban levő tagok számával. Például: ha a sorban 4 cella van és ha az első szám a cellában 4, te csak 1 felhőkarcolót fogsz látni, mert a 4 emeletes felhőkarcoló eltakarja az 1 emeletes, a 2 emeletes és a 3 emeletes felhőkarcolókat. Skyscrapers - felhőkarcolók szabályok:
|
Skyscrapers - felhőkarcolók Parkokkal
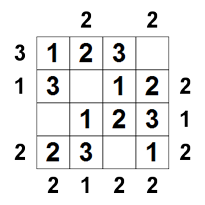 | A Skyscrapers - felhőkarcolók rejtvényben lehetnek Parkok (üres cellák). Skyscrapers - felhőkarcolók Parkokkal szabályok:
|
Sum Skyscrapers-felhőkarcolók összege
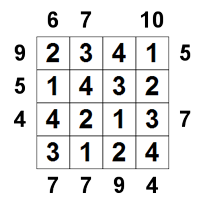 | A számok végig a Felhőkarcolók összege rács mentén jelzik a magasság összegét a látható épületeknél. Sum Skyscrapers - felhőkarcolók összege szabályok:
|
Binary-bináris
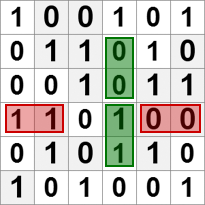 | Töltsd ki a rácsot nullákkal (0-k) és egyesekkel (1-ek) ameddig csak ugyanannyi nullák és egyesek lesznek minden sorban és minden oszlopban. Binary-bináris szabályok:
|
Téglák
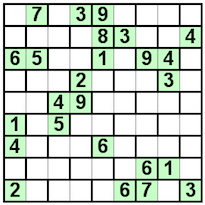 | A Téglák hasonló a Latin négyzethez. A rejtvény mezői párokra vannak osztva, ezáltal úgy néz ki, mint egy téglafal. Téglák szabályai
|

