Przewodnik po obrazkach logicznych - Rozwiązywanie łamigłówek
Przykład 1: Rozwiązywanie łatwego obrazka
(używając SLS - ang. single line solving, rozwiązywanie jednej linii)
Rozwiązywanie obrazków jest procesem eliminacji: wyliczasz, gdzie muszą znajdować się kolorowe kwadraty, a gdzie nie mogą. Jeśli będziesz tak postępował, kolejne rzędy i kolumny dadzą się kolejno rozszyfrować.
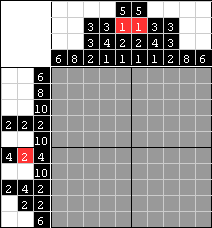 | To jest łamigłówka, którą zamierzamy rozwiązać. Składa się ona z trzech kolorów. Dwa kolory będą tworzyć obrazek (czarny i czerwony), a trzeci kolor będzie białym tłem. Rozwiążemy ten obrazek używając metody SLS (z ang. Jedno-Liniowe Rozwiązywanie) co oznacza, że będziemy się skupiać tlyko na jednej linii na raz. |
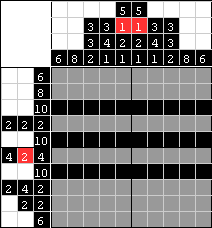 | Zacznijmy rozwiązywanie: Nie ma ustalonego punktu startowego. To, co robimy zazwyczaj na początku, to przejrzenie rzędów i kolumn w poszukiwaniu pól z najwyższymi numerami. W tej łamigłówce widzimy, że są 3 rzędy poziome, które zawierają po 10 przylegających czarnych kwadratów, a skoro okno ma 10 pól szerokości, to nie potrzeba kalkulatora, aby stwierdzić, że w tych rzędach wszystki kwadraty będą zamalowane. |
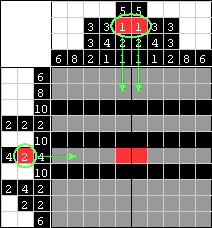 | Następnie szukamy oczywistych pól. W tym przypadku są to 2 czerwone kwadraty przebiegające poziomo. Kiedy przyjrzysz się numerowanym polom na górze okna, zobaczysz, że są tylko 2 kolumny pionowe, które zawierają czerwone kwadraty. Stąd 2 czerwone pola nie mogłyby znaleźć się nigdzie indziej niż w tych 2 kolumnach. |
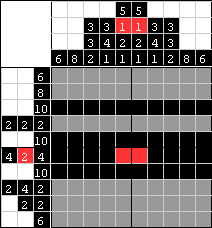 | Teraz możemy bez problemu zapełnić 2 czarne bloki po 4 pola znajdujące się po obu stronach czerwonych pól, gdyż są tam dokładnie po 4 wolne pola. Tak, moglibyśmy po prostu spojrzeć na ten rząd i powiedzieć 4+2+4=10 i wypełnić cały rząd od razu. To właśnie pokazuje, że nie ma ustalonego sposobu rozwiązywania, którego należy się trzymać. Wybór sposobu zeleży od tego, na co najpierw wolisz zwrócić uwagę. |
| Teraz spójrzmy na pierwszy rząd poziomo, w którym znajduje się blok 6 czarnych kwadratów. Obrazki pokazują, że mamy pięć możliwości rozmieszczenia tego bloku. Jednak widać, że bez względu na to, która możliwość będzie poprawna, 2 kwadraty zaznaczone zielonym X będą czarne, gdyż są zamalowane w każdym przypadku, więc nie ma możliwości, aby nie były czarne. | |
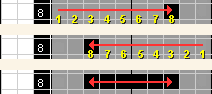 | Zamalowujemy więc te 2 kwadraty w najwyższym rzędzie na czarno. Następnie widzimy, że ostatni rząd jest taki sam, czyli możemy zamalować te same 2 kwadraty. Później, używając tej samej dedukcji, możemy zamalować 6 z wymaganych 8 kwadratów w drugim rzędzie. |
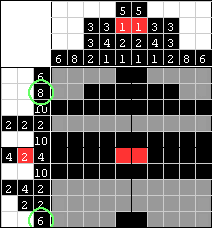 | Najprostszą metodą aby to zrobić jest policzenie 8 kwadratów od lewej strony i zamalowanie ósmego pola, pózniej policzenie 8 kwadratów od prawej strony i zamalowanie ósmego pola, a na koniec zamalowanie pól pomiędzy nimi. |
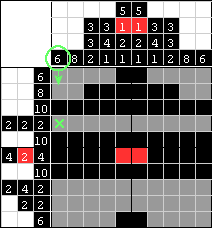 | Spójrzymy teraz na pierwszą kolumnę, która ma zawierać blok 6 czarnych kwadratów. Aby blok był nieprzerwany, musimy wstawić czarny kwadrat w miejsce zielonego X. |
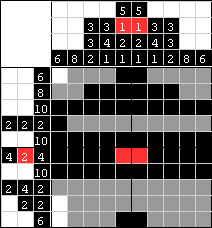 | Po zamalowaniu tego pola mamy 5 z 6 wymaganych pól dla tej kolumny. To oznacza, że jeszcze tylko 1 czarne pole będzie potrzebne, więc górny kwadrat i dwa dolne muszą być białe, gdyż blok 6 pól nie sięgnie tak daleko. |
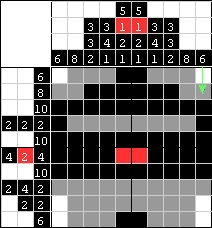 | Ostatnia kolumna jest identyczna jak pierwsza, czyli możemy zrobić to samo. |
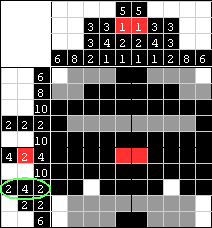 | Teraz spójrzmy na rząd z numerami wziętymi w zielone kółko. Wiemy, że bloki tego samego koloru muszą mieć canajmniej jedną przerwę pomiędzy sobą, więc prosta arytmetyka powie nam, że wszystkie 10 pól można odpowiednio zamalować. 2 czarne + 1 białe + 4 czarne + 1 białe + 2 czarne = 10 |
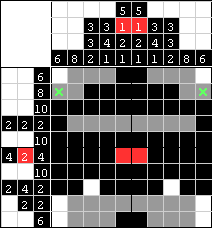 | To dało nam wymagane bloki po 6 pól w pierwszej i ostatniej kolumnie, więc możemy zamalować na biało 2 kwadraty zaznaczone zielonym X. |
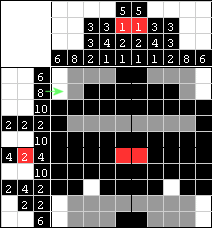 | Drugi rząd od góry obecnie zawiera tylko 8 pól dostępnych, które można zamalować, a skoro rząd wymaga bloku 8 czarnych kwadratów, to można założyć, że oba szare kwadraty po bokach 6 wcześniej zamalowanych pól również muszą być czarne. |
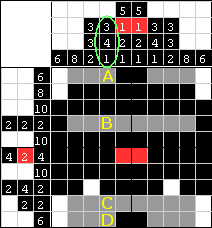 | Teraz spójrzmy na czwartą kolumnę. Potrzeba nam 3,4 i 1. Skoro mamy już blok 4 czarnych pól pomiędzy B a C, a najdłuższy dozwolony blok w tej kolumnie ma mieć 4 pola i tylko jeden blok o tej długości jest wymagany, to to jest właśnie to. Ponieważ potrzebujemy conajmniej jedno pole puste z każdej strony bloku, to pola B i C muszą być białe. Gdzieś poniżej bloku 4 czarnych pól znajduje się jeszcze jedno czarne pole, a skoro D jest jedynym wolnym polem odkąd C zamalowaliśmy na biało, to pole D musi być czarne. Podobnie, na górze ma się znajdować blok 3 czarnych pól, a skoro B jest białe, to A musi być czarne. |
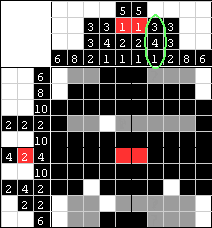 | Teraz sytuacja jest taka, jak na obrazku i ponownie widzimy, że mamy drugą kolumnę taką samą jak przed chwilą rozwiązana. Więc robimy z nią to samo, co w poprzednim kroku. |
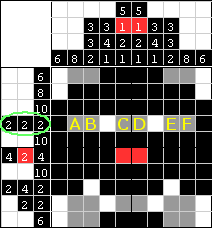 | W tym rzędzie potrzebujemy bloki 2 czarnych pól. 2 białe pola które już mamy pomogą nam w rozwiązaniu. Mamy po jednym czrnym polu na każdym końcu rzędu, a skoro bloki mają mieć po 2 pola to pola A i F muszą być czarne. Zostaje nam tylko jedno miejsce w tym rzędzie gdzie zmieściłby się blok 2 pól, więc C i D także należy zamalować na czarno. Ponieważ mamy już 3 wymagane bloki, to B i E muszą być zamalowane na biało. |
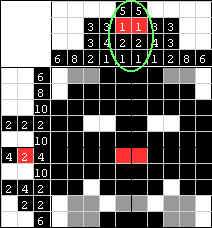 | Wszystkie wymagane kolorowe pola są już wypełnione w tych kolumnach, a więc szare pola należy zamalować na biało. |
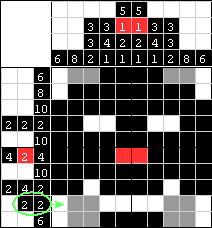 | Wskazówki w tym rzędzie to 2 i 2. Są tylko 2 dostępne dla nich miejsca. Zamalujmy je na czarno. |
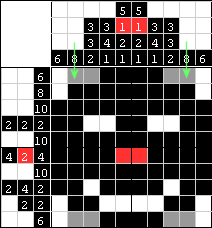 | Obie kolumny mają już 8 zapełnionych pól, więc pozostałe szare pola muszą być zatem białe. |
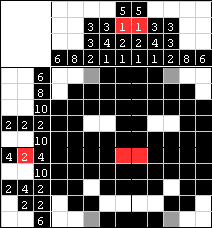 | Teraz pozostały nam 2 szare kwadraty na górze i 2 szare na dole. Bez względu na to, czy skorzysta się ze wskazówek podanych z boku, czy u góry planszy, okaże się, że wszystkie te pola muszą być czarne. |
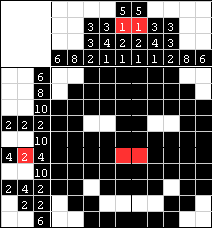 | Wszystkie pola są wypełnione. Skąd wiemy, że rozwiązanie jest prawidłowe? |
 | Jeśli wszystko rozwiązane jest poprawnie, wszystkie numerowane pola i linie na planszy znikną pozostawiając tylko obrazek. Miłej zabawy! |

